Well, the link doesn’t load for me

Yeah, they’re doing an upgrade right now. Yes, it’s the Maths explanation - -25 is the correct answer.

-5**2 is apparently -25 because of the order of operations)

Which is correct

I wasn’t going to reply any more, but I see now you don’t understand terms either, so one more time for old time’s sake (and maybe you might finally get it)…

perhaps you have sunk so much time

You know teachers don’t get paid for helping students outside class time right?

assume I must be wrong

No assumption needed. What you are proposing is literally impossible. I’ve been saying that all along.

Take another look at my third and fifth paragraphs.

Ok…

I’m not saying you can take any expression and get the same answer by doing addition before multiplication

And so far you haven’t been able to show it works for any expression at all! Not even one expression! Just like I said would happen.

All I am saying is that you can still use numbers to solve problems with an altered order of operations

And I said you can’t, and you haven’t! All you did was put brackets around the multiplication to make sure we were still following the only order of operations that works! You have still not shown an actual instance where one can actually do addition first and get a right answer, not one! The idea that one could use addition first as an “alternate order of operations” is thus pure fantasy, just like I’ve been saying all along. It’s literally impossible.

for example (x+4)(x-2) would no longer need brackets

Yes it would! (x+4) is one term - that’s what the brackets means - “these things are all together”. If you remove that, because “addition first”, it’s now two terms, so the whole expression is two terms (instead of one), x, and 4(x-2) (which is a mistake people make when they write 8/2(2+2) as 8/2x(2+2) - just turned 2 terms into 3 terms and changed the answer!). Every example you’ve done so far you’ve used brackets to escape from having to do addition first, and the very same thing would therefore apply here - no brackets, no escaping “addition first” approach, brackets before addition leads to x+4(x-2)=x+(4x-8) =5x-8, which is not the product of (x+4) and (x-2).

The presence of brackets where there would be none otherwise does not invalidate my point

No, the fact that you’ve not been able to show a single instance of where addition before multiplication would work does. You can’t show “a way to solve this in an addition first world” when it’s literally impossible for an “addition first world” to exist in the first place.

I never wrote 15²+50²

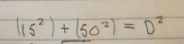
…and I removed the brackets to show that addition first doesn’t work (since you keep putting in brackets to revert “addition first” back to the only order of operations that actually works).

It can still be used to “study of the measurement, properties, and relationships of quantities and sets using numbers and symbols”

And you’ve still not shown how. Every example you’ve used so far you’ve put in brackets to your (supposed) “addition first” so that we were evaluating it using the only order of operations that works. In other words, no, you can’t use “addition first” to “study of the measurement, properties, and relationships of quantities and sets using numbers and symbols” - you used the regular order of operations to do it! You haven’t shown a single example of where addition first could be used to do it.

you need to use that order of operations

You need to use an order of operations that gives a correct answer, of which there is only one - a fact you keep trying to avoid.

different order of operations and a+2xa-2 simplifies to a^2-4

No it wouldn’t, cos now you’re ignoring terms as well. As per my earlier working out, it would simplify to 5x-8 unless you also changed the definition of terms. Do you see yet why it’s impossible to have an “alternate order of operations”?

All I am trying to say is that that their math, with a different order of operations, would be no less useful then our math

And you’ve completely failed to show a single instance where this is true - which is what I’ve been saying all along, it’s impossible to have another set of order of operations that works. You keep pre-supposing it’s possible, but then add brackets to the multiplications so that we follow the actual correct order of operations, the only order of operations that works.

my only claim is that you can still use a different order of operations to manipulate numbers and solve real world problems

And you’ve still failed to solve a single problem using addition first, because it’s still a fact it’s literally impossible to do so.

was still able to come to the correct answer

by using the only order of operations that works. i.e. multiplication before addition.

Now I really am done - I’m not going any further down this rabbit hole of whatever other Maths you may not understand either (this post it was Terms - who knows what’s next)…

It’s only a wrong answer

Really? You want to do that again? Ok, fine… If I have 1 2 litre bottle of milk, and 4 3 litre bottles of milk - i.e. 2+3x4 - how many litres of milk do I have?

you would with the standard order of operations

The definition of 5 as being 1+1+1+1+1 has nothing to do with order of operations.

there is no law of the universe that makes 5 look like that

No, but there is a rule of Maths which defines it.

switch the definitions of the symbols 5 and 4 if we did it all at once and revised old math expressions to match the new standard

In other words everything would be the same as now but we just switched the notation around. I already said that to you a while back. Now you’re getting it.

there is no reason the order of operations is what it is other than that is how someone decided to write it

Got nothing to do with how it’s written - Maths is written differently in many different countries, and yet the underlying order of operations rules are universal.

I’m not saying you can take any expression and get the same answer by doing addition before multiplication

And if it’s not the same answer then it’s wrong. You’re nearly had it.

I’m saying you can take any problem and get the correct answer by doing addition before multiplication

And I told you you can’t. Waiting on a proof from you. Start with 2+3x4 - show me how you can get the correct answer by doing addition first - it’s a nice simple one. :-)

that means I would use the expression 2+(3x4) because 2+3x4

They’re literally the same thing.

All I am saying is that you can still use numbers to solve problems with an altered order of operations, or by altering any part of the system of notation

And I told you that it’s impossible. Changing the notation doesn’t change the Maths.

As you can see, I used my altered math notation to find the correct answer

BWAHAHAHAHA! Nope! I see you putting brackets around the multiplication to make sure it gets done first - same as if you hadn’t used brackets at all! It’s the exact same notation we use now, just with some redundant brackets added to it! And, predictably, you left the addition for last.

Ok, let’s take your example and do addition first (like you claimed can be done)…

15²+50²=15x15+50x50=15x65x50=48,750. But 15²+50² is 2,725 according to my calculator. Ooooh, different answers - I wonder which one is right… I wonder which one is right…???

Thanks for proving it can only be done by following the order of operations rules (just like I’ve been saying to you all along). Bye now.

I think you misunderstand my argument

No, you demonstrably didn’t understand mine, which is, what you are saying is impossible, but you’re still saying it’s possible.

I could use still math to solve a real-world problem with an altered order of operations

No, you can’t. You already tried to do addition first in 2+3x4 and found out why it doesn’t work. Ever since then you’ve been ignoring that result and pretending that there’s some other way to make it work. No, there isn’t. As long as multiplication is defined in terms of addition (i.e. 3x4=3+3+3+3) then it’s impossible to get a right answer unless you do multiplication before addition.

You could still do anything you can do with regular math, if you had a different order of operations

No, you can’t. Again, you already proved you can’t.

Do you need me to calculate something, to prove it to you?

Go ahead - I’m not holding my breath. I already told you why it literally can’t work. But note that adding brackets isn’t changing the order of operations - brackets are already part of the order of operations. Writing 2+3x4 as 2+(3x4) is exactly the same thing.

BTW just to FURTHER prove your “addition first” doesn’t work, look at this example…

3x4+2=3x6=18. But earlier you did 2+3x4=5x4=20 - not even the same answer in an “addition first” world! Welcome to why it’s impossible to make addition-first work. But knock yourself out - you’re welcome to try! 😂

The order of operations is just part of a system of notation

No, it isn’t. It’s part of the rules of Maths. Notation is how you write it - underlying that is how Maths actually works. This is embodied in the rules of Maths.

is inherently arbitrary

Completely fixed, and a result of the way the operators are defined - that was the only “arbitrary” bit, deciding what the operators were and what they were going to mean, but once you did that then the order of operations rules were already written for you (having already been determined as soon as you made the definitions of the operators in the first place).

number 5 has no inherent meaning behind it other than the convention of how we interpret it

Again, not a convention, a rule of how to interpret it. You can’t just decide to interpret 5 as four, or again, you end up with wrong answers. The rules of Maths prevent you from getting wrong answers. You found that out yourself when you tried to do addition first in 2+3x4.

Noted that you didn’t answer my question - the answer is I have 14 litres of milk. 2+3+3+3+3=14 litres. When you did “arbitrary addition first”, you got 20, which is wrong, which is why no other order of operations rules work than the ones we have.

You can’t change how equations work and then expect all equations to work the same after the change

In actual fact the point is that they will except for what ever your new notation is. e.g. if we instead defined + to mean multiply, and x to mean add, then we would do + before x, and again, that would be the only order of operations which works. i.e. the only order which gives us 14 litres.

that doesn’t mean there is anything fundamentally wrong with having a different system of writing equations in which operations are executed in a different order

No, and if you did that, you would again arrive at only one order of operations rules which works, cos I still have 14 litres, and the Maths in this new system still has to give an answer of 14 litres, not 20.

Our whole system of writing equations is just a convention

Nope, it’s all rules, found in any Maths textbook, and if you don’t obey the rules you get wrong answers (like you did when you got 20).

But there is no fundamental truth behind it

Yes there is - I have 14 litres, and only 1 set of order of operations rules gives that answer.

only that it is simpler for the majority of use cases

If you follow the rules of Maths then it is correct for every use case. That’s why they exist in the first place.

2+(4x3) gives the right answer, with addition coming before multiplication

If we rewrote all of Maths so that addition came before multiplication, then no, 2+3x4 would no longer mean what it does now (because + and x would have to mean something different to what they do now in order for the order to be swapped). The order of operations rules come directly from the definitions. You can’t just say “we’ll do addition first” without having defined what addition is now, nor multiplication. In a world where addition comes before multiplication, that means multiplication is no longer shorthand for addition (because that’s the very thing which means we have to do multiplication before addition, so it can’t be true anymore if now we’re doing addition first).

Let’s take an imaginary scenario where we now use x for add, and + for multiply. That would indeed mean that + has to be done before x, but note that + now means multiply. That means your “addition first” 2+(3x4) is what we currently mean by 2x(3+4) which is 14. Now take away the brackets (since I don’t use brackets when adding up the milk! Just 2+3x4). Your addition-first 2+3x4 is equivalent in our multiplication-first world to 2x3+4 which equals 10 - the wrong answer! So now you’ve created a world where we have to add brackets to things just to get the right answer! Why would you even want to do that when it works the way it is? The whole point to having order of operations rules is to not have to add brackets!

5+5+5+5=20. What is the issue with that?

That it’s wrong. If I have 1 2 litre bottle of milk, and 4 3 litre bottles of milk - i.e. 2+3x4 - how many litres of milk do I have? Without even doing the arithmetic, just count it up and tell me how many litres there is.

Actually I’m educating and hoping people will stop arguing about it. You can take it on board or not. You actually nearly had it.

Also, your comments will show up in search results for all eternity unless you delete them.

I agree it needs to be more clearly defined

It’s clearly defined in any Maths textbook you pick up.

2y, should take higher priority simply because it cannot be any further resolved or simplified

Bingo!

That is not the case with, say, 2(3+1)

It’s the same thing, where y=3+1.

1/7y. Is the coefficient 7, or is it 1/7? i.e. Is that 1/(7y)

Yes, it’s 1/(7y) as per the definition of Terms.

Either way, if that’s not the the standard understood by everyone

It’s the standard in literally every Maths textbook.

I’ve even had people share a snip from some book that states this as fact

A Maths textbook.

However, this is not standardized

It’s standard in every Maths textbook.

there is no reason to treat it as such just because a few people assert it is should be

The “few people” are Maths teachers and Maths textbook authors.

It doesn’t make sense at all to me that implied multiplication would be treated any differently

There’s no such thing as implicit multiplication

They’re both the same operation

No, what people are calling “implicit multiplication” is either The Distributive Law - which is the first step in solving Brackets - or Terms - and neither of these things is “multiplication”. Multiplication literally refers to multiplication symbols only.

It’s why that symbol is not used by real mathematicians at all. It is just abundantly more clear what you’re saying if you use the fraction bar notation

The division symbol is used - it is not the same thing as a fraction bar.

x÷y(z) is the SAME as x÷y*z.

No, it’s the same as x÷(y*z).

There’s no mathematical or logical reason to treat it differently

Terms, The Distributive Law, are why it’s treated differently.

2(4)^2=(2x4)^2=8^2=64

Yes, that’s right. Brackets before Exponents, as per the order of operations rules.

You can’t distribute into a bracket

You know that’s literally what The Distributive Law says you must do, right? Unless you have a source somewhere saying there’s an exception?

Apparently you didn’t bother reading any of the links I gave you, so here’s one of the many textbooks which says you must distribute…

In case that’s unclear, that means that 2x² and 2(x)² aren’t the same thing (since 2(x)=(2x) by definition).

wolfram syntax

You know Wolfram disobeys The Distributive Law, right? I know I’m not the only one who knows this. Is that why you’re insisting your way is right? Cos they’re known to be wrong about this.

If you respond with more bullshiting,

You call quoting Maths textbooks “bullshiting”?

So, no sources. Got it.

The original Greek “-ikos” was both the feminine singular when refering to “the art” (the whole field)

In modern English it’s The Arts - plural as it refers to all types of art (music, painting, etc.).

whether the s was thruncated appears random

I’m not sure North Americans would appreciate being called “random”. 😂 Just the other day I was surprised when I saw a Canadian who used an American spelling, and when I asked him about it he said he was pretty much forced to because programming uses American spelling.

useage

Usage

several thousand year old grammar (from a region remote enough that we forgot about it for several centuries) with syntax rules not present in the original.

Did you miss the part where it says it’s a borrowed word?

Just out of curiosity, what is the first 2 doing in “2(2+2)”…? What are you doing with it? Possibly multiplying it with something else?

Distributing it, as per The Distributive Law. Even Khan Academy makes sure to not call it “multiplication”, because that refers literally to multiplication signs., which, as I said, there aren’t any in this expression - only brackets and division (and addition within the brackets).

I feel bad for your students

My students are doing well thanks.

I doubt anyone is going to accept links to your blog as proof that you are correct

You mean the blog that has Maths text book references, historical Maths documents, and proofs? You know proofs are always true, right? But thanks for the ad hominem anyway, instead of any actual proof or evidence to support your own claims.

8/2(1+3) even if they technically are meant to be evaluated the same

But 8/2(1+3) isn’t a fraction. The / - the computing equivalent of ÷ (which can only be written using Unicode on a computer, so a bit of a pain to use compared to / )- is an operator, which means they’re 2 separate terms. A fraction bar is a grouping symbol, which means it’s 1 term. In this particular case it doesn’t matter, but if it appeared in a bigger expression then it absolutely does matter. The way to write 8/2(1+3) as a fraction inline is to add extra brackets. i.e. (8/2(1+3)) - because brackets are also a grouping symbol.

And as for distributive law vs multiplication, maybe this is just taking for granted a thing that I learned a long time ago, but to me they’re just the same thing in practice

Bu they’re not, for the same reason. Firstly, the Distributive Law isn’t multiplication at all - which only applies literally to multiplication symbols - it applies to bracketed terms (i.e. is a single term which needs to be distributed) - and secondly it applies to a single term, whereas multiplication applies to 2 terms (one before and one after). Anyone who talks about 2(1+3) needing to be “multiplied” has already made the mistake that is going to lead to a wrong answer (unless they just happen to “multiply” before they divide, which is an accidental way to get the right answer).

if I was factoring something

Indeed, that is the precise reason the Distributive Law exists - they are the opposite operation to each other! Anyone who adds a multiplication symbol has broken up the factorised term, again leading to the wrong answer.

I’m just being a bit lose with the terminology

Yeah, and that’s all I was pointing out in the first place - please don’t use “implicit multiplication”. The term itself - i.e. it includes “multiplication” - leads people to do it wrong (because they treat it as multiplication, not brackets, then argue about the precedence of “multiplication”!). It needs to die!

this can rapidly get unreadable once you nest more than a few parens,

Well that’s why the rules of Terms ab=(axb) and The Distributive Law a(b+c)=(a*(b+c))=(ab+ac) exist to begin with - less brackets! :-) Imagine having to write a fraction as (1/(axb)) all the time!

(8)/(2(1+3)) is obviously different than (8/2)(1+3)

Correct, though a lot of people treat it as the latter (yet another way to do it wrong - doing division before brackets) because they figure the 8/2 is “outside the brackets”, but in fact only the 2 is, because the slash separates them as being 2 terms.

We agree that the two situations are separate

Ok, that’s a start.

but the first result is 4 ÷ a the second result is 4a

Exactly! So when a=2 then 4÷a=2, and 4a=8, which isn’t the same thing. Welcome to why 2a and 2xa (and therefore also 2.a) aren’t the same thing.

I use the dot as an expression of the same term rather than separate.

But that is incorrect. A dot is used for multiplication. i.e. it separates terms. If you use a . for 2.a, then you are writing the same thing as 2xa, not the same thing as 2a.

This is matter of my notational convention

Well, that’s fine enough if you keep it to yourself, but don’t use it in anything anyone else is going to read, or you’re going to run into the issues I just pointed out

“Wrong answers” only according to our current order of operations

No, according to arithmetic.

math still works if you, for example, make additions come first

No, it doesn’t - order of operations proof. The only way it could work with addition first is if we swapped the definitions of addition and multiplication around… but then we still have the same order of operations, all we’ve done is swapped around what we call addition and multiplication!

there is no ‘high truth’ behind it.

There is when it comes to order of operations.

That proof for the order of operations sure seems to rely a lot on our current order of operations

Doesn’t use order of operations at all. It only uses the definitions of the operators. i.e. 3x4=3+3+3+3 by definition. i.e. nothing to do with order of operations.

If I have 1 2l bottle of milk, and 4 3l bottles of milk, how many litres of milk do I have? It can be solved by simply adding them up - again, nothing to do with order of operations here, just simple addition. Now, write it out as a mathematical expression which uses multiplication, and tell me which order of operations gets you the right answer. Voila! Welcome to how we worked out what the order of operations rules had to be.

That’s an after the fact justification

You got some sources with dates in them to show it was “after”, and not, you know, before?